Running an ANCOVA to see if there is a difference in the adjusted means (least square means LSM) of my dependent variable between two areas (Area1 and Area2) while controlling a variable as a covariate. I tried two ways, with aov() and lm(). I would like to ensure I am interpreting the results correctly. All assumptions have been met for an ANCOVA and there is no difference in slopes (used lm(dependent~Area*covariate)).
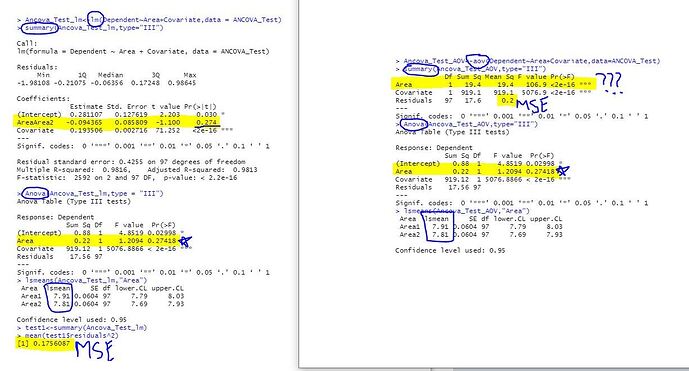
With the lm(dependent~Area+covariate). I see that there is no difference between the areas (p=0.274) using both the summary() and Anova() function and that Area2 is 0.09 less than Area1 (Can see this rounded up in lsmean as well). My Mean square error is 0.175. I can see my covariate and dependent variable also have a significant relationship (p = <0.2e-16) which is an assumption of the ANCOVA anyways.
With the aov(dependent~Area+covariate). I that using the summary function, I have a significant difference in the means between the areas (p = <0.2e-16); however, in the Anova(), I have the same non-significant result as the lm model (p=0.274). My mean square error is 0.2, which I am assuming is just the rounded up number and the same as the lm function. My LSmeans are the same as the lm function.
So I am assuming my lm model is correct; however, I don't understand why the summary() gave me a wildly different result. I initially tried it to get my MSE before finding out that I can use model$residuals^2 to get it from the lm().
Also, am I interpreting the above correctly and have my code correct (i.e., dependent ~ Area + Covariate)? Area 1 adjusted mean is 7.91 and Area 2 is 7.81. MSE is 0.2. This difference is not statistically significant (p=0.274).
Thanks for any input!