I created two GAM models looking at the relationship between precipitation depth and the increase in stream discharge under two treatment scenarios, however, the 95% confidence interval appears to be much too narrow and does not include most of the residuals.
Since I had very few precipitation events with a precipitation depth greater than 20 mm, I removed these events from the dataset and focused only on the relationship between precipitation events less than 20 mm using the code
prePrecip20 <- pre.dat$PrecipAdjust[which(pre.dat$PrecipAdjust < 20)]
preIncrease20 <- pre.dat$IncreaseAdj[which(pre.dat$PrecipAdjust < 20)]
postPrecip20 <- post.dat$PrecipAdjust[which(post.dat$PrecipAdjust < 20)]
postIncrease20 <- post.dat$IncreaseAdj[which(post.dat$PrecipAdjust < 20)]
I then created a GAM model comparing the relationship between precipitation events greater than 20 mm and the corresponding increase in stream discharge for these events under both a pre-treatment (i.e., "preGAM20") and post-treatment (i.e., "postGAM20") scenario using the code:
preGAM20 <- gam(preIncrease20 ~ s(prePrecip20),method = "REML")
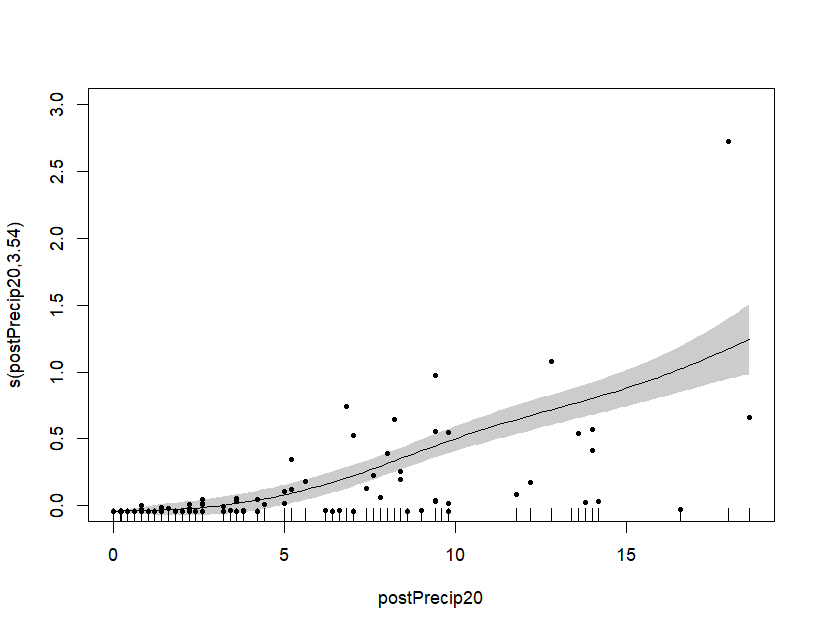
postGAM20<- gam(postIncrease20 ~ s(postPrecip20), method = "REML")
I then plotted each GAM model using the code:
plot(preGAM20, shade = TRUE, residuals = TRUE, pch = 20, ylim = c(0,3))
plot(postGAM20, shade = TRUE, residuals = TRUE, pch = 20, ylim = c(0,3))
I believe that the command "shade = TRUE" above should display 95% confidence intervals, however, the above code returned the following plots:
Plot 1: preGam20
Plot 2: pstGAM20
As shown in both of the plots above there are many residuals that lay outside of the shaded confidence interval. This is leading me to believe that the code "shade = TRUE" is not providing a 95% confidence interval as I expected that it would.
Also could somebody please explain what the residuals on my plot are showing? Each plot contains 2577 individual observations, so I am not quite sure what the 66 points in the preGAM plot and 67 points in the postGAM plot are showing?
TIA