3D datavizualisation and color

MoLo · December 6, 2020, 7:31pm

Good morning Everyone!

A pleasure to be with you again.

today I have an urgent need to visualize my data for futhur analysis.

I am working on Human Activities Recognition data
I have a database with 5 groups of variables (mean, std, mad, max, min) and each variables are split in 3 other (X, Y, Z) that means I have 15 variables: meanX, meanY, meanZ, stdX,stdY,stdZ, ....... and a last one (16th) that i will use for color: Activite.
I would like to data vizualise the dataframe in on graphic. I use the package rgl for 3D output, but I can't set all the 15 variables.

i am open for any tip on how I can produce the graphic.
for example: we can have the five variables on each of the three axes X,Y,Z and the color will be the 16th variables:Activite

Please help me! thank you in advance

I am using rgl package but I still can put all the variables together.

MoLo · December 6, 2020, 7:32pm

This is the representation of my data set

AlexisW · December 6, 2020, 7:53pm

Are you sure it's a good idea to plot all these variables together? First, I'd expect much of this is redundant, as the standard deviation, the mad, and the max-min are all measures of dispersion, is there any reason why they wouldn't show more or less the same thing? Intuitively, I would start with a simple boxplot of the means separating X, Y and Z, as well as the activity. Separately, perhaps another boxplot with the sd or the mad could give a different information. But of course no point in putting these on the same plot, since they have different scales.

The interpretation also depends a lot on the meaning of X, Y, and Z.

If truly these were independent variables (but I really doubt it considering their names), you could try a dimensionality reduction such as PCA to bring them on a 3D plot.

MoLo · December 6, 2020, 7:58pm

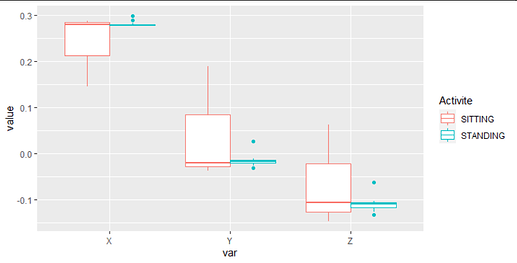
This is a dput of an extract of my database. hope it can help

dput(extrait)
structure(list(meanX = c(0.28858451, 0.27841883, 0.27965306,
0.27917394, 0.27662877, 0.27719877, 0.27945388, 0.27743247, 0.27729342,
0.28058569, 0.27688027, 0.27622817, 0.278457, 0.27717497, 0.29794572,
0.27920345, 0.27903836, 0.2801349, 0.27773106, 0.27556818, 0.27756171,
0.27715238, 0.2756763, 0.2792002, 0.28171549, 0.27899267, 0.27573444,
0.14450396, 0.28725164, 0.2799976), meanY = c(-0.020294171, -0.016410568,
-0.019467156, -0.026200646, -0.016569655, -0.01009785, -0.019640776,
-0.030488303, -0.021750698, -0.0099602983, -0.012721805, -0.021441302,
-0.020414761, -0.014712802, 0.027093908, -0.023020143, -0.014800378,
-0.013916951, -0.018210718, -0.016979698, -0.014318487, -0.017983328,
-0.021264234, -0.017714427, -0.011910678, -0.014531029, -0.01801884,
0.18926326, -0.037455064, -0.019484036), meanZ = c(-0.13290514,
-0.12352019, -0.11346169, -0.12328257, -0.11536185, -0.10513725,
-0.11002215, -0.12536043, -0.12075082, -0.10606516, -0.10343832,
-0.10820234, -0.11273172, -0.10675647, -0.061668123, -0.12208028,
-0.11684896, -0.10637048, -0.10918803, -0.11142918, -0.10787724,
-0.10660117, -0.11080122, -0.10916135, -0.10287513, -0.10659617,
-0.10677578, 0.062769317, -0.14597431, -0.10572355), stdX = c(-0.9952786,
-0.99824528, -0.99537956, -0.99609149, -0.99813862, -0.99733496,
-0.99692104, -0.99655926, -0.99732847, -0.99480344, -0.99481511,
-0.99824595, -0.99913488, -0.99918834, -0.98864079, -0.99683904,
-0.99694116, -0.99769492, -0.99749074, -0.99781139, -0.99790424,
-0.99776322, -0.99786211, -0.99838929, -0.99853388, -0.99805969,
-0.99925496, -0.90429967, -0.98291504, -0.99281839), stdY = c(-0.98311061,
-0.97530022, -0.96718701, -0.9834027, -0.98081727, -0.99048681,
-0.96718593, -0.96672843, -0.96124532, -0.9727584, -0.97307692,
-0.98721376, -0.98468004, -0.99052638, -0.8166986, -0.97484812,
-0.98186562, -0.98751567, -0.99322197, -0.9905223, -0.99431129,
-0.98995727, -0.99009076, -0.98730784, -0.98848901, -0.98606983,
-0.99366888, -0.18193654, -0.89160489, -0.94035041), stdZ = c(-0.91352645,
-0.96032199, -0.97894396, -0.9906751, -0.99048163, -0.99542003,
-0.98311783, -0.98158533, -0.98367156, -0.98624387, -0.98535702,
-0.99272659, -0.99627424, -0.99336501, -0.90190653, -0.98338551,
-0.98257653, -0.99040744, -0.99612795, -0.99762104, -0.99595166,
-0.99658567, -0.99459257, -0.99083159, -0.99318367, -0.99342424,
-0.9941888, -0.44315051, -0.94143811, -0.98149266), madX = c(-0.99511208,
-0.99880719, -0.99651994, -0.99709947, -0.99832113, -0.9976274,
-0.99700268, -0.99648525, -0.99759576, -0.99540462, -0.99550927,
-0.99825127, -0.99907654, -0.99921135, -0.98895795, -0.99709389,
-0.99721998, -0.99801432, -0.99790305, -0.99820522, -0.99836517,
-0.99829082, -0.99833345, -0.99886852, -0.99867433, -0.99805916,
-0.99940654, -0.90110019, -0.98441781, -0.99309238), madY = c(-0.98318457,
-0.97491437, -0.96366837, -0.98274984, -0.97967187, -0.99021769,
-0.96609671, -0.96631315, -0.95723623, -0.97366322, -0.97394796,
-0.98599654, -0.98293702, -0.99068725, -0.79428042, -0.97333193,
-0.98161964, -0.98795448, -0.99271072, -0.98946983, -0.99360447,
-0.9896687, -0.98947266, -0.98677131, -0.98854392, -0.98519239,
-0.99362014, -0.11081268, -0.89137296, -0.93692706), madZ = c(-0.92352702,
-0.95768622, -0.97746859, -0.9893025, -0.99044113, -0.9955489,
-0.98311627, -0.98298176, -0.98437928, -0.98564195, -0.98517247,
-0.99318188, -0.99641031, -0.99216753, -0.8880146, -0.98406535,
-0.98133604, -0.99219012, -0.99649182, -0.99719303, -0.99559481,
-0.99670045, -0.99448451, -0.98963739, -0.99328718, -0.99501788,
-0.99358295, -0.40059935, -0.93336072, -0.9806691), maxX = c(-0.93472378,
-0.94306751, -0.93869155, -0.93869155, -0.94246912, -0.94246912,
-0.94098663, -0.94098663, -0.94059758, -0.94002751, -0.94002751,
-0.94390578, -0.94390578, -0.94332286, -0.92597669, -0.9417158,
-0.9417158, -0.94207598, -0.94487012, -0.94566163, -0.94147242,
-0.94147242, -0.94456672, -0.94367519, -0.94255883, -0.94255883,
-0.94288961, -0.93189578, -0.93189578, -0.935389), maxY = c(-0.56737807,
-0.55785126, -0.55785126, -0.57615889, -0.56917385, -0.56568389,
-0.56568389, -0.57263824, -0.56417505, -0.55459369, -0.55459369,
-0.57142214, -0.56970419, -0.56935747, -0.44846574, -0.57093916,
-0.56349958, -0.56349958, -0.57509103, -0.57334183, -0.57295816,
-0.57295816, -0.57528783, -0.56780337, -0.56386922, -0.56386922,
-0.57586911, 0.042098681, -0.49953681, -0.56525476), maxZ = c(-0.74441253,
-0.81840869, -0.81840869, -0.82971145, -0.82470529, -0.82276614,
-0.81718902, -0.81718902, -0.82352693, -0.81585037, -0.81585037,
-0.82069493, -0.82503369, -0.8225147, -0.73057881, -0.81763455,
-0.8242149, -0.81589176, -0.81589176, -0.82658225, -0.82002259,
-0.81751965, -0.81751965, -0.82543702, -0.81539879, -0.81539879,
-0.82266472, -0.3365258, -0.82469972, -0.82253173), minx = c(0.85294738,
0.84930787, 0.84360895, 0.84360895, 0.84909512, 0.84909512, 0.85104022,
0.85032778, 0.85032778, 0.84544241, 0.84544241, 0.85053227, 0.85206858,
0.85203494, 0.84866648, 0.84866648, 0.85257303, 0.84985145, 0.84715408,
0.84715408, 0.85161294, 0.84968627, 0.84968627, 0.85001518, 0.85252893,
0.85044026, 0.85044026, 0.71647623, 0.82636555, 0.84772493),
minY = c(0.68584458, 0.68584458, 0.68240094, 0.68240094,
0.68324978, 0.69558572, 0.67434716, 0.67041013, 0.67041013,
0.68475694, 0.68475694, 0.6865276, 0.6865276, 0.6926473,
0.68064999, 0.68064999, 0.6888947, 0.69387601, 0.69259112,
0.69259112, 0.69476646, 0.68945922, 0.68945922, 0.69190301,
0.69354066, 0.69188515, 0.69127318, 0.65581306, 0.65581306,
0.66274101), minZ = c(0.81426278, 0.82263681, 0.83934417,
0.83786929, 0.83786929, 0.84592156, 0.83359122, 0.83238324,
0.83238324, 0.83845531, 0.83845531, 0.84601343, 0.84601343,
0.8463496, 0.83820463, 0.83820463, 0.83839767, 0.83839767,
0.84722607, 0.84750921, 0.84750921, 0.84986038, 0.84137235,
0.84137235, 0.84726168, 0.84156459, 0.84156459, 0.80898559,
0.80898559, 0.83760928), Activite = c("STANDING", "STANDING",
"STANDING", "STANDING", "STANDING", "STANDING", "STANDING",
"STANDING", "STANDING", "STANDING", "STANDING", "STANDING",
"STANDING", "STANDING", "STANDING", "STANDING", "STANDING",
"STANDING", "STANDING", "STANDING", "STANDING", "STANDING",
"STANDING", "STANDING", "STANDING", "STANDING", "STANDING",
"SITTING", "SITTING", "SITTING")), row.names = c(NA, 30L), class = "data.frame")

MoLo · December 7, 2020, 3:00am

Yes yes yes
You are definitely right.
I am considering PCA and Ascendant Clustering as well..

How can I produce the boxplot for the mean separating X, Y, Z and as well as the Activity?

And, I still wish to put all the variables on the same plot just to see how possible it is to visualize all the data together.

Again, Thank you in advance

AlexisW · December 7, 2020, 3:34am

Unless I'm missing something I just don't think it's possible to plot 15 variables on a 2D or 3D plot.

Else you have to use some kind of heatmap format and/or summary statistic (for example mean of each column), but what representation makes sense totally depends on what the variables really represent and what the research question is.

For the boxplot you can do that easily with ggplot2, if you first pivot your data in a long format:

library(tidyverse)

extrait %>%
  pivot_longer(cols = 1:15,
               names_to = c("stat", "var"),
               names_pattern = "([a-z]+)([XYZ])") %>%
  filter(stat == "mean") %>%
  ggplot() +
  geom_boxplot(aes(x = var, color = Activite, y = value),
               position = "dodge")

Depending on the meaning of X, Y, Z, it can make sense to first center and scale them (so they're all on a scale of -1 to +1).

MoLo · December 9, 2020, 12:24pm

thank you for your answer.
I had a health issue that's why I didn't answer right away.

I am using Jupiter Notebook for R, and it doesn't recognize the function pivot_table, even when I call the libraries tidyr and tidyverse.

the goal is to be able to predict the Activite (walking,sitting...) by doing a Clustering and Scoring.

please help me.

AlexisW · December 9, 2020, 3:45pm

That could be a problem, you will need libraries to do many things, if your Jupyter setup doesn't work properly you can't work correctly.

I would start with the idea that all these variables could be very correlated and the actual problem have a low dimensionality: try simply plotting the first 3 PCs and see if the Activités cluster naturally.

Either on the PCA results or the raw data, you can try several classic clustering methods such as K-means and k-nearest neighbors.

If you're indeed in a prediction problem, don't forget to first separate a training set and a testing set, so that you can evaluate your results in an unbiased way at the end.

You can take a look at that free, online, book to get detailed explanations.

system · December 30, 2020, 3:46pm

This topic was automatically closed 21 days after the last reply. New replies are no longer allowed.

If you have a query related to it or one of the replies, start a new topic and refer back with a link.