Issues with Estimating Parameters in Gaussian Time Series Data Using R

[smaanan]

I am working on a project involving time series data with Gaussian noise, and I am encountering an issue with parameter estimation. Specifically, my estimated parameter psi differs significantly from the true value used in the data generation.

I generate Gaussian noise data using the following function in R:

simulate_data_gaussian <- function(T, a0, b0, psi0, sigma0) {
  epsilon <- rnorm(T - 1, mean = 0, sd = sigma0)
  y <- numeric(T)
  e <- numeric(T)
  e[1] <- rnorm(1, mean = 0, sd = sigma0)
  y[1] <- a0 + b0 * 1 + e[1]
  for (t in 2:T) {
    e[t] <- psi0 * e[t-1] + epsilon[t-1]
    y[t] <- a0 + b0 * t + e[t]
  }
  return(y)
}

I use this objective function to estimate parameters a, b, and psi:

f_objective <- function(a, b, psi, y, T) {
  residuals <- y[2:T] - a - b * (2:T) - psi * (y[1:(T-1)] - a - b * (1:(T-1)))
  return(sum(residuals^2) / T)
}

The complete code for the simulation is below:

# Simulated data (Gaussian)
set.seed(123)
T <- 100  # Sample size
a0 <- 1
b0 <- 2
psi0 <- 0.5
sigma0 <- 1
y <- simulate_data_gaussian(T, a0, b0, psi0, sigma0)

# Objective function f(a,b,psi)
f_objective <- function(a, b, psi, y, T) {
  residuals <- y[2:T] - a - b * (2:T) - psi * (y[1:(T-1)] - a - b * (1:(T-1)))
  return(sum(residuals^2) / T)
}


# Analytical solution for a and b in terms of psi
solve_ab_psi <- function(psi, y, T) {
  # Construct the system of linear equations for a and b
  A <- matrix(0, nrow = 2, ncol = 2)
  b_vec <- numeric(2)
  
  for (t in 2:T) {
    A[1, 1] <- A[1, 1] + 1 + psi^2
    A[1, 2] <- A[1, 2] + t + psi * (t - 1)
    A[2, 1] <- A[2, 1] + t + psi * (t - 1)
    A[2, 2] <- A[2, 2] + t^2 + (t - 1)^2
    
    b_vec[1] <- b_vec[1] + y[t] + psi * y[t-1]
    b_vec[2] <- b_vec[2] + t * y[t] + (t - 1) * psi * y[t-1]
  }
  
  # Solve for a(psi) and b(psi)
  solution <- solve(A, b_vec)
  a_psi <- solution[1]
  b_psi <- solution[2]
  
  return(c(a_psi, b_psi))
}

# Function to compute f(a(psi), b(psi), psi)
f_psi <- function(psi, y, T) {
  ab <- solve_ab_psi(psi, y, T)
  a_psi <- ab[1]
  b_psi <- ab[2]
  return(f_objective(a_psi, b_psi, psi, y, T))
}

# Generate psi values and evaluate f(psi)
psi_values <- seq(-1, 1, by = 0.01)
f_values <- sapply(psi_values, f_psi, y = y, T = T)

# Plot f(psi)
library(ggplot2)
df <- data.frame(psi = psi_values, f_value = f_values)
ggplot(df, aes(x = psi, y = f_value)) +
  geom_line() +
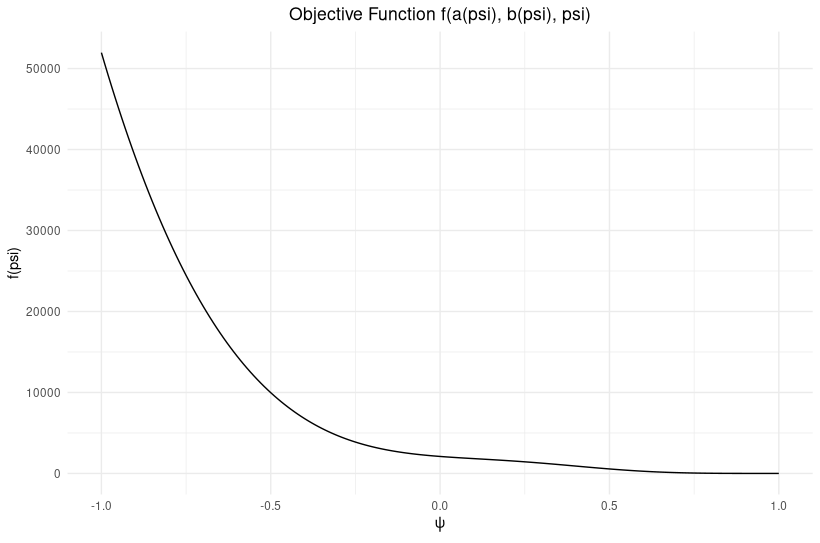
  labs(title = "Objective Function f(a(psi), b(psi), psi)", 
       x = expression(psi), y = "f(psi)") +
  theme_minimal() +
  theme(plot.title = element_text(hjust = 0.5))

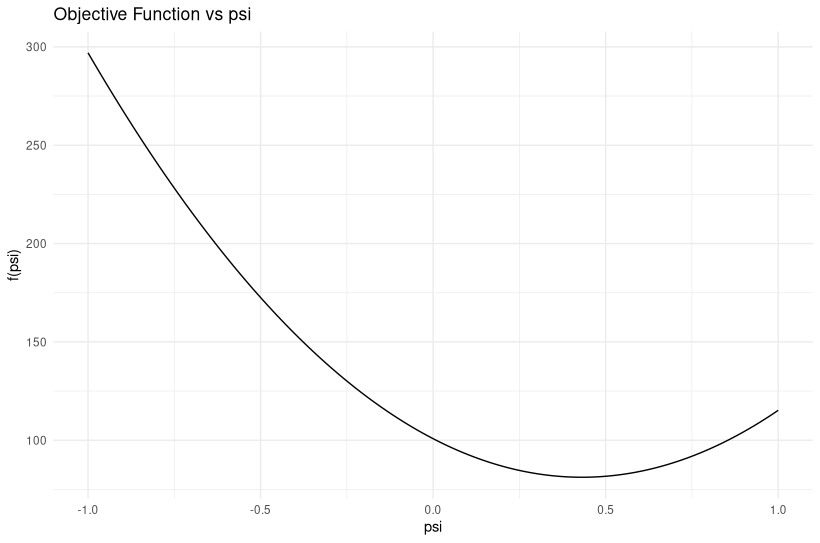
And the resulting estimations are shown in the figure below:

Issue: Despite generating data with psi0=0.5, my estimated psi is significantly different from 0.5 (0.98). I validated the generated data and objective function, but the discrepancy persists.

Question: Can someone help me understand why the estimated psi is different from the true value psi0? What might be going wrong in my estimation process?

[alvarosg]

Your solve_ab_psi function does not look good to me.
In the simple case psi0 = 0, it should be the same as a standard linear regression with white noise, but the system defined in solve_ab_psi is not.

Also, if I understood what you are trying to do, maybe
e[t] <- psi0 * e[t-1] + epsilon[t-1]
should probably be
e[t] <- psi0 * y[t-1] + epsilon[t-1]

[startz]

The specification of the AR(1) process for the errors is correct.

[startz]

I realize your question may really be about the programming rather than the problem, but in case it helps...

library(orcutt)
y <- simulate_data_gaussian(T, a0, b0, psi0, sigma0)
t<-1:T
m <- lm(y~t)
> cochrane.orcutt(m)
Cochrane-orcutt estimation for first order autocorrelation 
 
Call:
lm(formula = y ~ t)

 number of interaction: 3
 rho 0.45053

Durbin-Watson statistic 
(original):    1.09164 , p-value: 1.351e-06
(transformed): 1.98377 , p-value: 4.268e-01
 
 coefficients: 
(Intercept)           t 
   0.858102    2.006589 

works nicely.

[smaanan]

I edited the code as follows and now it gives much better results:

# Set seed for reproducibility
set.seed(123)

# Define parameters
T <- 100
a0 <- 1
b0 <- 2
psi0 <- 0.5
sigma0 <- 1

# Simulate data
simulate_data_gaussian <- function(T, a0, b0, psi0, sigma0) {
  e <- rnorm(T, 0, sigma0)
  y <- numeric(T)
  y[1] <- e[1]
  for (t in 2:T) {
    y[t] <- a0 + b0 * t + psi0 * y[t-1] + e[t]
  }
  return(y)
}

y <- simulate_data_gaussian(T, a0, b0, psi0, sigma0)

# Define objective function
f_objective <- function(a, b, psi, y) {
  T <- length(y)
  sum_sq_res <- 0
  for (t in 2:T) {
    res <- y[t] - a - b * t - psi * y[t-1]
    sum_sq_res <- sum_sq_res + res^2
  }
  return(sum_sq_res)
}

# Solve for a and b given psi
solve_ab_psi <- function(psi, y) {
  T <- length(y)
  X <- matrix(0, nrow = T-1, ncol = 2)
  X[,1] <- 1
  X[,2] <- 2:T
  Y <- y[2:T] - psi * y[1:(T-1)]
  beta <- solve(t(X) %*% X) %*% t(X) %*% Y
  return(list(a = beta[1], b = beta[2]))
}

# Function to compute f(psi)
f_psi <- function(psi, y) {
  ab <- solve_ab_psi(psi, y)
  return(f_objective(ab$a, ab$b, psi, y))
}

# Generate psi values and compute f(psi)
psi_values <- seq(-1, 1, by = 0.01)
f_values <- sapply(psi_values, function(psi) f_psi(psi, y))

The value that minimizes f(psi) is much closer the the true psi0.