Right this is expected. Scenario:
A cohort of customers install the app on 1/1/21. I have a field that tracks the cumulative revenue of the cohort day to day. E.g. if they spend 100 on day 1 (Jan 1st) then 110 on day2 (Jan2) then growth rate is 1.1. A growth rate of 1 implies no growth.
So, yes, min(exdata$GrowthRate) should be close to 1 or even 1 in this data set.
Are you suggesting I scale this in some way?
In fact in the sample you posted, about 14 percent of the data is 1.0.
Hm. Yes this could be expected. Do you think maybe I should just remove them?
Having played around a little with the data you posted, let me say wow...no wonder you're having trouble. It's really hard to model.
After you get a working model, what are you going to use it for?
Goal is to predict future revenue using these growth rates. Welp, thanks for taking a look anyway! Will post here if I have any success.
Part of what's going on is that there is a lot of noise in the growth rates. A lot of them are 1.0. But quite a few are above 1.5. Can that happen on one day? Sure. But it can't be sustained. I would aggregate the data to monthly and see if that makes things work better.
The expectation is that as Day increases, GrowthRate will decrease. I.e. new customers spend more than older ones. Yeah might try weekly or monthly grouping. Thanks for your contributions!
I'll be curious to hear if something works out.
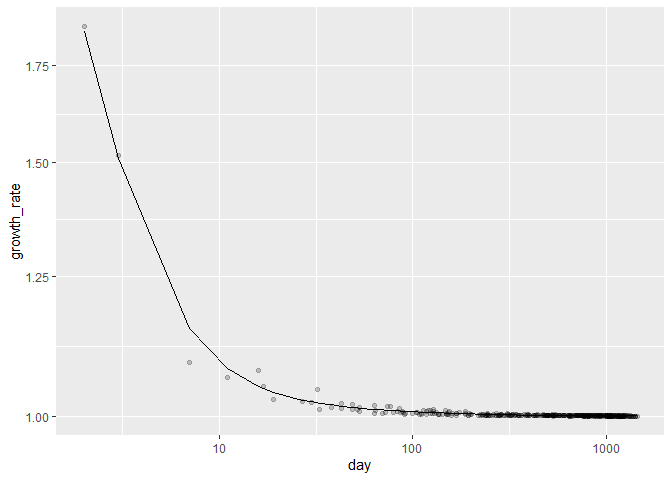
I am able to get a pretty good fit. Looks good even from log-log perspective.
The critical pieces!
library(tidyverse)
df <- structure(list(day = c(668, 228, 872, 715, 159, 337, 935, 278,
822, 808, 647, 272, 169, 929, 507, 38, 241, 776, 836, 477, 3,
503, 729, 654, 526, 341, 239, 447, 608, 732, 829, 225, 246, 553,
641, 699, 805, 434, 796, 136, 243, 197, 319, 287, 751, 570, 537,
440, 155, 888, 283, 72, 778, 795, 148, 765, 74, 309, 63, 286,
942, 89, 997, 864, 64, 808, 130, 895, 824, 2, 152, 545, 250,
529, 907, 909, 11, 941, 168, 358, 880, 315, 771, 647, 528, 295,
894, 269, 739, 467, 439, 325, 504, 111, 106, 604, 493, 549, 608,
913, 496, 588, 30, 695, 350, 277, 688, 427, 353, 83, 118, 379,
257, 915, 187, 548, 352, 828, 793, 647, 501, 649, 830, 105, 674,
400, 998, 33, 753, 85, 950, 16, 395, 418, 314, 711, 978, 852,
219, 701, 324, 718, 790, 619, 471, 328, 27, 88, 576, 849, 690,
338, 392, 389, 123, 806, 945, 847, 960, 329, 345, 657, 43, 123,
493, 502, 650, 534, 230, 460, 281, 920, 861, 776, 114, 908, 645,
497, 849, 503, 429, 91, 111, 313, 433, 882, 703, 611, 792, 160,
128, 277, 187, 486, 321, 528, 150, 571, 153, 382, 420, 193, 529,
118, 513, 711, 108, 550, 489, 709, 243, 473, 32, 984, 493, 661,
494, 570, 812, 887, 17, 77, 126, 546, 137, 525, 400, 238, 232,
494, 143, 151, 251, 285, 53, 150, 70, 984, 135, 805, 284, 19,
52, 366, 53, 747, 63, 393, 121, 79, 223, 767, 532, 244, 875,
981, 531, 92, 931, 49, 798, 304, 751, 49, 245, 763, 188, 591,
754, 365, 128, 86, 132, 786, 271, 938, 759, 198, 716, 601, 43,
7, 482, 299, 168, 779, 201, 308, 237, 99, 195, 1000, 397, 897,
261, 921, 732, 174, 563, 636, 1293, 1199, 1196, 1188, 1156, 1021,
1077, 1123, 1200, 1264, 1322, 1128, 1150, 1206, 1408, 1194, 1162,
1075, 1155, 1108, 1091, 1059, 1126, 1008, 1015, 1073, 1024, 1171,
1096, 1218, 1022, 1286, 1063, 1172, 1047, 1411, 1386, 1190, 1341,
1051, 1017, 1010, 1219, 1190, 1193, 1038, 1006, 1171, 1422, 1162,
1186, 1147, 1195, 1366, 1162, 1376, 1097, 1353, 1008, 1010, 1010,
1037, 1225, 1155, 1208, 1258, 1309, 1241, 1225, 1111, 1041, 1244,
1354, 1092, 1022, 1041, 1068, 1048, 1205, 1327, 1057, 1233, 1173,
1075, 1055, 1238, 1256, 1442, 1210, 1056, 1227, 1050, 1009, 1085,
1304, 1056, 1145, 1016, 1130, 1202), growth_rate = c(1, 1.00306502480229,
1, 1.00076851094002, 1.00148339803649, 1.00045123354242, 1.00020383148751,
1.00040965825011, 1, 1.00031779508266, 1.00066482023658, 1.00346513143248,
1.00425818538852, 1.0000656266777, 1.0001181890034, 1.01397743783103,
1.00139112715821, 1.00081959407673, 1.00009809095611, 1.00044236058947,
1.51727840805678, 1.00121675720201, 1.00008407903631, 1.0002592753402,
1.000030898582, 1.00018747698804, 1.00076380264933, 1.00036102684816,
1.00014528643822, 1.00062904941809, 1.00035187773298, 1.00111580249086,
1.00128571600603, 1.00016768160482, 1.00031901973645, 1.00023357797553,
1, 1.00041471510241, 1.00035864164816, 1.00240475926205, 1.00171028989878,
1.00424915891236, 1.00132476644926, 1.00221292841008, 1.00050907600983,
1.00044491397686, 1.00159525492273, 1.00180564684984, 1.00736657558218,
1, 1.0026255455024, 1.00522416568146, 1.00053636280677, 1.00036357279992,
1.00848394039131, 1.00006750976761, 1.01480026218821, 1.00284373740064,
1.00450411011131, 1.00221965194253, 1, 1.00539973548843, 1, 1.0005005471049,
1.0090122482097, 1, 1.00323230127301, 1.00032245565711, 1.00011354681804,
1.86253085002583, 1.00493992498232, 1.00241870746302, 1.00078006797611,
1.00098571121886, 1.00020587722401, 1, 1.06357635769067, 1.00002460995387,
1.00391720899917, 1.00119656881149, 1, 1.00107863162601, 1.00105245561527,
1.00008689169125, 1.0012783975488, 1.00154555116813, 1.00007359702218,
1.00084802657738, 1.00041660475254, 1.00011183062243, 1.00063625619285,
1.00135232882137, 1.00028938223461, 1.00315936176759, 1.00532364235978,
1.00030657799902, 1.00061342100673, 1.00030571104406, 1.00011715885948,
1, 1.00047974561815, 1.00025430105801, 1.02198934501457, 1.00010416687303,
1.00059014062243, 1.00047780779104, 1.00002874641645, 1.00111112119003,
1.00048837107964, 1.00754570558638, 1.00755154435772, 1.00254002012421,
1.00159784391408, 1.00007543627185, 1.00378184040293, 1.0003705762736,
1.00036115588121, 1.00022933557137, 1.00029709263616, 1.00009829460504,
1.00140576471426, 1, 1.00005859317971, 1.00525400638917, 1.00011859424543,
1.00056320336456, 1.00035496874922, 1.00990917838274, 1.00003017505772,
1.01216605816059, 1.00009508876079, 1.07550081281054, 1.0009053688873,
1.00033679896333, 1.00256186904405, 1.00024334207759, 1, 1.00006156466836,
1.0010976624319, 1.00012077834143, 1.00128712135851, 1.0001649556448,
1, 1.00026425686049, 1.00101428907282, 1.0018129199355, 1.0232877524855,
1.00781265091469, 1.00088597626466, 1.00009409356407, 1.00015668455482,
1.00207944494908, 1.0008364573296, 1.00025217525085, 1.00851816270978,
1.00016567699951, 1.0005450520462, 1, 1.00005352201724, 1.00265963863935,
1.00278084396241, 1.00039100408185, 1.0119269039859, 1.00348007368147,
1.00028324293254, 1.00093475581609, 1, 1.00049601640004, 1.00093369723894,
1.00060643539062, 1.00045179198477, 1.0001781622325, 1.00046194521224,
1, 1.00837269520819, 1.00020635263389, 1, 1.00059134502924, 1.00037811956032,
1.00041897791628, 1.00042567344896, 1.00315548828686, 1.00468000407093,
1.00117636662781, 1.00060407694, 1.00024651907264, 1.00040214420152,
1.00026572826846, 1, 1.00339182682076, 1.00677033400408, 1.00155795560629,
1.00709197798949, 1.00038408589383, 1.00044811349183, 1.00130624808202,
1.00213573137913, 1.00033829641388, 1.00181882251488, 1.00135268084575,
1.00021867236035, 1.00124421720953, 1.00167528270764, 1.00177999673699,
1.00111286906933, 1.00010382083562, 1.00281412834574, 1.00056084643116,
1.0003141068177, 1.00008783630833, 1.00295297113833, 1.00164418951503,
1.04254942398587, 1.00003463339853, 1.00026114582086, 1.00050325855951,
1.00027372250255, 1.00087794701574, 1, 1.00013019716725, 1.04849400865707,
1.01576530751161, 1.00464667740791, 1.00018645212712, 1.00232488088618,
1.00004828157946, 1.00003981436502, 1.00154051691592, 1.00300130371862,
1.00123014317303, 1.00178350354365, 1.00280125310909, 1.00058260459095,
1.00046312111938, 1.01338850447998, 1.00324092586586, 1.00435413084373,
1.00045526312721, 1.00239458582682, 1, 1.00072778216623, 1.02606789744901,
1.01114042578054, 1.00064178777718, 1.0070741027695, 1.00012247290823,
1.01674249234518, 1.00242915312699, 1.00914195421065, 1.00600241912814,
1.00186581948127, 1, 1.0009766510536, 1.00356182186649, 1.00061069533127,
1.0004239892255, 1, 1.00423354957881, 1, 1.01840023022722, 1.00014520016924,
1.00092286729759, 1.00006763577849, 1.01050940078589, 1.00083492872673,
1, 1.00212321384912, 1.00042771571448, 1.00005841382969, 1.00091286897932,
1.01020966954758, 1.00636232332844, 1.00629472490287, 1.00006023350623,
1.0006479378345, 1, 1, 1.00192163655976, 1.00037288252448, 1.00079827070308,
1.02036948481831, 1.08953748979677, 1.00005419459345, 1.00091099942311,
1.00158239355759, 1.00056725169743, 1.00254767904885, 1.00323409855214,
1.00082718448862, 1.00453370970986, 1.000723554716, 1.00017946087637,
1.00177142955793, 1.00002646875663, 1.00176656474078, 1.00062703527375,
1.00005493403402, 1.00516938013927, 1.00041653082443, 1.00014928977913,
1.00020721162875, 1, 1, 1, 1.00006564860028, 1, 1, 1, 1, 1.00003044890406,
1, 1, 1, 1, 1, 1, 1, 1.0001045870866, 1.0000969223039, 1.00003558158276,
1, 1.00014456034634, 1, 1.00006005834686, 1.00001996732182, 1,
1, 1, 1.00006796560531, 1.00002505991713, 1.00033215470201, 1.00025086529074,
1, 1, 1.00005211550219, 1, 1, 1, 1, 1.00005113850633, 1.00003684287429,
1.00007239452958, 1.00009072804825, 1, 1, 1, 1, 1.00018251149956,
1, 1, 1, 1, 1, 1, 1, 1, 1.00002144750158, 1, 1.00002257182718,
1, 1.0001890858105, 1, 1, 1, 1, 1, 1, 1.00001721483368, 1.00005676253354,
1.00012229728215, 1, 1.00020620900577, 1, 1, 1, 1, 1.00044288582059,
1.00002461203578, 1, 1.00008842939096, 1.00006595081859, 1, 1.00007436380507,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1.00080787992677, 1, 1, 1.00013030856866,
1.00022073762073, 1, 1.00001973205065, 1.00005050803594)), row.names = c(NA,
-400L), class = "data.frame")
# log-log with growth - 1 is approx. linear
print(
df %>% ggplot() + aes(day, growth_rate - 1) + geom_point() +
scale_x_log10() + scale_y_log10()
)
#> Warning: Transformation introduced infinite values in continuous y-axis
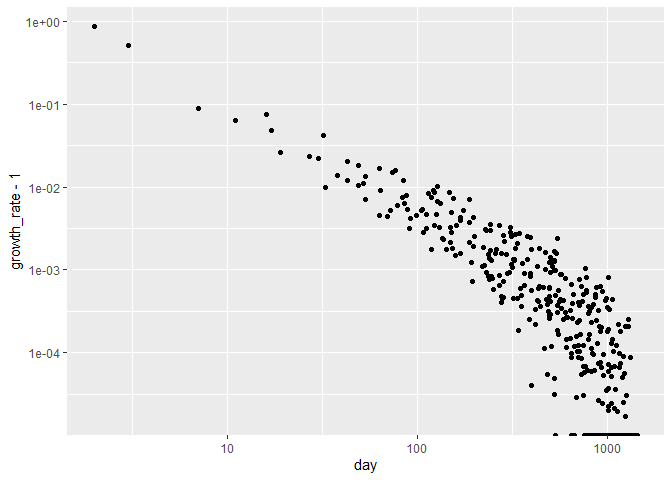
# the reason why we need to subtract 1 is so growth can continue to decrease through
# orders of magnitude 10^-1, 10^-2, etc.
# add columns for the transformed variables
df <- df %>%
mutate(growth_rate_m1 = growth_rate - 1, day_plus_3 = day + 3)
# filtered so we can model
dfm <- df %>% filter(growth_rate > 1)
# fit model and add predicted growth to df
model <- lm(
log(growth_rate_m1) ~ poly(log(day_plus_3), 3),
data = dfm,
weights = growth_rate_m1 # scale high values more
)
summary(model) %>% print()
#>
#> Call:
#> lm(formula = log(growth_rate_m1) ~ poly(log(day_plus_3), 3),
#> data = dfm, weights = growth_rate_m1)
#>
#> Weighted Residuals:
#> Min 1Q Median 3Q Max
#> -0.156213 -0.019200 -0.010042 0.005349 0.143044
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -6.76221 0.06968 -97.049 < 2e-16 ***
#> poly(log(day_plus_3), 3)1 -26.26473 0.96626 -27.182 < 2e-16 ***
#> poly(log(day_plus_3), 3)2 -2.83995 0.66531 -4.269 2.63e-05 ***
#> poly(log(day_plus_3), 3)3 -3.43207 0.32168 -10.669 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.02707 on 305 degrees of freedom
#> Multiple R-squared: 0.9805, Adjusted R-squared: 0.9803
#> F-statistic: 5107 on 3 and 305 DF, p-value: < 2.2e-16
df <- df %>% mutate(pred_growth = exp(predict(model, df)) + 1)
# plot
print(
df %>%
ggplot() +
geom_point(aes(day, growth_rate), alpha = 0.2) +
geom_line(aes(day, pred_growth))
)
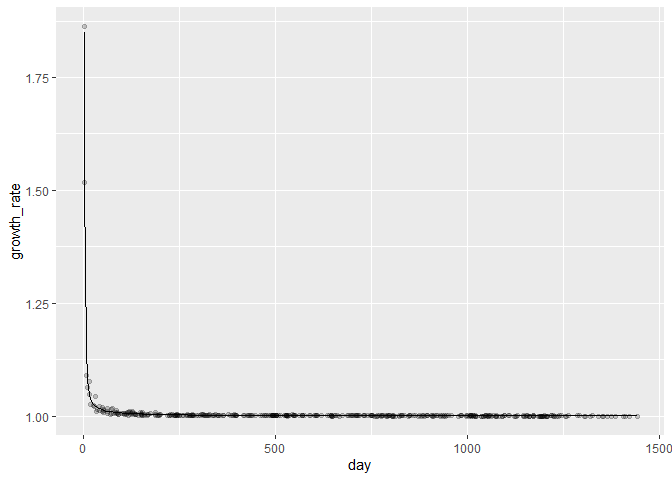
print(
df %>%
ggplot() +
geom_point(aes(day, growth_rate), alpha = 0.2) +
geom_line(aes(day, pred_growth)) +
scale_x_log10() + scale_y_log10()
)
Created on 2022-02-03 by the reprex package (v2.0.1)
WOW! This is beautiful. Thank you Arthur. I'm looking forwards to replicating this. Will let you know how that goes. Thanks very much, I've taken a lot from this.
Might have some follow up Q's as I try to build this in my env.
Hi Arthur. I had a chance to try this approach out on my real data and it really does do well, even on test data! I'm attempting to reinforce my understanding of this approach and fill in some blanks so wanted to ask some follow ups...
model log(growth - 1). To capture the exponential relationship, it's important to have a quantity that goes towards zero so when we take the log, the log continues to decrease through the orders of magnitude 10^-1, 10^-2, 10^-3,
This makes sense, thanks for suggesting this.
weight the regression with the growth rate
I got confused here. Have never used weighted regression before and I did some research and watched some videos. I get the idea at a conceptual level - place less weight on outliers in higher variance areas. My question is, why weight with growth rate, which is already the target variable? E.g. why not weight inversely with predictor variable Day? Or even 1- 1/day? (This is very shot in the dark, just trying to understand). Putting it another way:
1 / Day?day_plus_3?
df <- df %>% mutate(growth_rate_m1 = growth_rate - 1, day_plus_3 = day + 3)
Why weight the regression? There is a lot of action in just the first 100 days, and then over 1000 additional days with near zero growth. We are minimizing the sum of square errors in log of growth. The log will squish and stretch such that it treats high values of growth and very low value democratically. Look at the first plot in my reprex with the log-log axes and imagine a regression line through it. All those points on the right for days > 100 are going to exert a LOT of influence on the regression line in the log-log space. But in fact those points are all essentially zero growth. The shape of the regression line from days 1 through 100 is what I care about most. I don't want the regression to give equal weight to a differences of 0.5 and 0.4 and 0.005 and 0.004. Therefore I weighted it. Is this the best choice of weight? I'm not sure.
I don't remember exactly why I chose days + 3. Maybe I had a zero value and I wanted to add a small constant so I could take the log. Maybe it made the curve a little bit more linear in the log-log plot.
Thanks again Arthur, I have a lot to go on with this post!
This topic was automatically closed 7 days after the last reply. New replies are no longer allowed.
If you have a query related to it or one of the replies, start a new topic and refer back with a link.