I want to use asymmetric Gaussian filter to smooth an image, because I don't want the equal smoothness in vertical and horizontal (with different size of standard deviation, σ). This means that I want a different σ for the vertical and horizontal, let's say σ_v = 0.001 and σ_h = 0.2.
For a "fixed" Gaussian filter I can do:
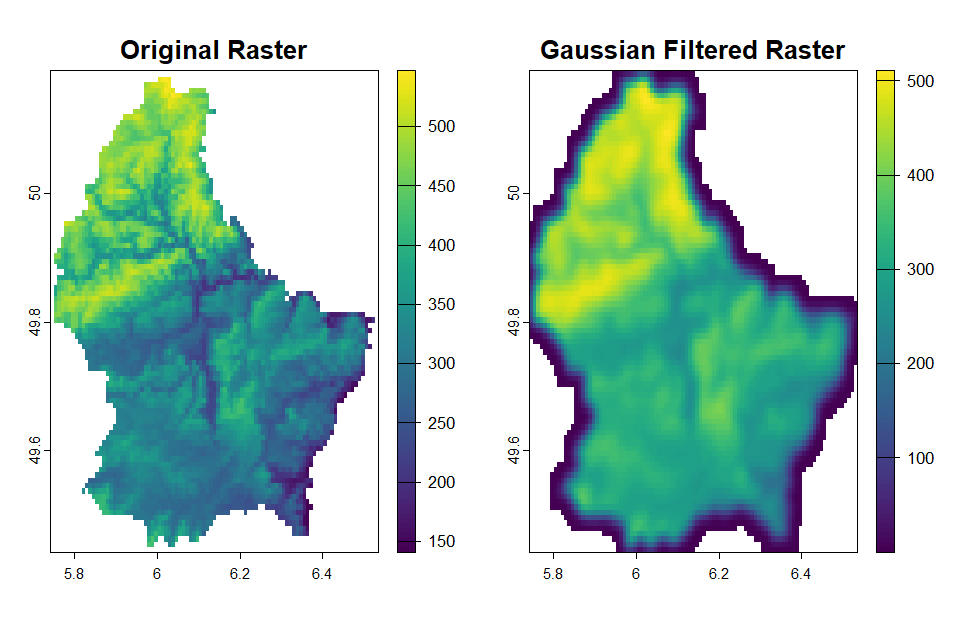
library(terra)
f <- system.file("ex/elev.tif", package="terra")
r <- rast(f)
gf <- terra::focalMat(r, 0.01, "Gauss")
r_gf <- terra::focal(r, w = gf, fun = "sum")
par(mfrow = c(1, 2))
plot(r, main = "Original Raster")
plot(r_gf, main = "Gaussian Filtered Raster")
and the result will be
How can I set different σ for the vertical and horizontal?
> sessionInfo()
R version 4.4.3 (2025-02-28 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 11 x64 (build 26100)
Matrix products: default
locale:
[1] LC_COLLATE=English_United States.utf8 LC_CTYPE=English_United States.utf8 LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C LC_TIME=English_United States.utf8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] terra_1.8-29
loaded via a namespace (and not attached):
[1] compiler_4.4.3 tools_4.4.3 rstudioapi_0.17.1 Rcpp_1.0.14 codetools_